R. S. Sharp
Lecturer, Department of Mechanical Engineering, University of Leeds, Leeds, LS2 9fT.}
(The M S . of this paper was received at the Institution on 10th August 1970 and accepted for publication on 17th May 1971. 2)
Resumo: São desenvolvidos modelos matemáticos de uma motocicleta e piloto dependentes de três suposições alternativas sobre o comportamento do pneu. São comparadas características de estabilidade deduzidas delas, e são estabelecidos requisitos mínimos para o modelo maiores do que os que foram satisfeitos anteriormente. Usando o mais sofisticado dos modelos, são calculados os efeitos das mudanças de projeto, e são discutidas as implicações do projeto.
Notação
(A), (B): Matrizes de coeficientes.
![Rendered by QuickLaTeX.com \[ \left. \begin{aligned} a, b, c, d, e \\ h, k, j, k, l \\ R_f, R_r, t \end{aligned} \right\} \quad \text{Dimensões lineares (Fig.1).} \]](https://renanxyz.com.br/wp-content/ql-cache/quicklatex.com-2ccee586dedfc20b475934795e0c98eb_l3.png)
![]() : Rigidez de curva dos pneus dianteiro e traseiro, respectivamente.
: Rigidez de curva dos pneus dianteiro e traseiro, respectivamente.
![]() : Rigidez de cambagem dos pneus dianteiro e traseiro, respectivamente.
: Rigidez de cambagem dos pneus dianteiro e traseiro, respectivamente.
![]() : Produto da inércia do chassi traseiro em relação aos eixos acima.
: Produto da inércia do chassi traseiro em relação aos eixos acima.
![]() : Aceleração devido à gravidade.
: Aceleração devido à gravidade.
![]() ,
, ![]() ,
, ![]() : Inércias do chassi dianteiro em relação aos eixos paralelos a
: Inércias do chassi dianteiro em relação aos eixos paralelos a ![]() (Fig.2) através do centro de massa (assumidos como eixos principais).
(Fig.2) através do centro de massa (assumidos como eixos principais).
![]() ,
, ![]() ,
, ![]() : Inércias do chassi traseiro em relação aos eixos paralelos a
: Inércias do chassi traseiro em relação aos eixos paralelos a ![]() (Fig.2) através do centro de massa.
(Fig.2) através do centro de massa.
![]() Momento polar de inércia do volante do motor.
Momento polar de inércia do volante do motor.
![]() : Momento polar de inércia da roda dianteira.
: Momento polar de inércia da roda dianteira.
![]() : Inércia de cambagem da roda traseira.
: Inércia de cambagem da roda traseira.
![]() : Momento polar de inércia da roda traseira.
: Momento polar de inércia da roda traseira.
![]() : Coeficiente do amortecedor de direção.
: Coeficiente do amortecedor de direção.
![]() : Massa do chassi dianteiro.
: Massa do chassi dianteiro.
![]() : Massa do chassi traseiro.
: Massa do chassi traseiro.
![]() ,
, ![]() ,
, ![]() : Componentes de velocidade angular do chassi dianteiro em relação aos eixos
: Componentes de velocidade angular do chassi dianteiro em relação aos eixos ![]() .
.
![]() ,
, ![]() ,
, ![]() : Componentes de velocidade angular do chassi traseiro em relação aos eixos
: Componentes de velocidade angular do chassi traseiro em relação aos eixos ![]() .
.
![]() ,
, ![]() : Coordenada e força generalizadas, respectivamente.
: Coordenada e força generalizadas, respectivamente.
![]() ,
, ![]() : Componentes das forças
: Componentes das forças ![]() e
e ![]() ao longo de
ao longo de ![]() e
e ![]() respectivamente.
respectivamente.
![]() : Velocidade de guinada (
: Velocidade de guinada (![]() ).
).
![]() : Soma de
: Soma de ![]() ,
, ![]() e
e ![]() , sendo a energia cinética total do sistema.
, sendo a energia cinética total do sistema.
![]() ,
, ![]() : Energias cinéticas dos chassis dianteiro e traseiro (excluindo a rotação das rodas) respectivamente.
: Energias cinéticas dos chassis dianteiro e traseiro (excluindo a rotação das rodas) respectivamente.
![]() : Energia cinética extra contabilizando a rotação das rodas.
: Energia cinética extra contabilizando a rotação das rodas.
![]() ,
, ![]() ,
, ![]() : Energias potenciais do chassis dianteiro, chassis traseiro e sistema total respectivamente.
: Energias potenciais do chassis dianteiro, chassis traseiro e sistema total respectivamente.
![]() : Velocidade lateral de 0 (
: Velocidade lateral de 0 (![]() ).
).
(![]() ): Matriz de colunas de amplitudes
): Matriz de colunas de amplitudes ![]() ,
, ![]() , etc.
, etc.
![Rendered by QuickLaTeX.com \[ \left. \begin{aligned} X_f, Y_f, Z_f \\ X_r, Y_r, Z_r \\ \end{aligned} \right\} \quad \text{Forças aplicadas nos pneus dianteiro e traseiro}\\ \]](https://renanxyz.com.br/wp-content/ql-cache/quicklatex.com-1f32a5b7f1a21230064bdac8cddcf3b4_l3.png)
nos pontos de contato com a estrada, respectivamente (Fig. 5).
![]() ,
, ![]() : Amplitudes de velocidade lateral e velocidade de guinada, respectivamente.
: Amplitudes de velocidade lateral e velocidade de guinada, respectivamente.
![]() ,
, ![]() ,
, ![]() ,
, ![]() : Coordenadas e velocidades do ponto de referência
: Coordenadas e velocidades do ponto de referência ![]() no sistema
no sistema ![]() .
.
![]() ,
, ![]() ,
, ![]() ,
, ![]() : Velocidades e acelerações do ponto de referência
: Velocidades e acelerações do ponto de referência ![]() no sistema
no sistema ![]() .
.
![]() ,
, ![]() : Forças laterais do pneu em estado estacionário.
: Forças laterais do pneu em estado estacionário.
![]() ,
, ![]() : Ângulos de deslizamento dos pneus dianteiro e traseiro, respectivamente.
: Ângulos de deslizamento dos pneus dianteiro e traseiro, respectivamente.
![]() : Ângulo de direção efetivo da roda dianteira (Fig. 6).
: Ângulo de direção efetivo da roda dianteira (Fig. 6).
![]() : Velocidade de direção (
: Velocidade de direção (![]() ).
).
![]() : Ângulo da cabeça de direção (Fig. 1).
: Ângulo da cabeça de direção (Fig. 1).
![]() : Velocidade do centro de massa do chassi dianteiro,
: Velocidade do centro de massa do chassi dianteiro, ![]() .
.
![]() : Velocidade do centro de massa do chassi traseiro,
: Velocidade do centro de massa do chassi traseiro, ![]() .
.
![]() ,
, ![]() : Coordenadas da posição angular das rodas dianteiras e traseiras, respectivamente.
: Coordenadas da posição angular das rodas dianteiras e traseiras, respectivamente.
![]() : Relação de marcha entre a roda traseira e o volante do motor.
: Relação de marcha entre a roda traseira e o volante do motor.
![]() : Coeficiente exponencial.
: Coeficiente exponencial.
![]() ,
, ![]() : Comprimentos de relaxamento dos pneus dianteiros e traseiros, respectivamente.
: Comprimentos de relaxamento dos pneus dianteiros e traseiros, respectivamente.
![]() : Torque de direção aplicado pelo piloto.
: Torque de direção aplicado pelo piloto.
![]() : Velocidade de rolamento (
: Velocidade de rolamento (![]() ).
).
![]() : Ângulo de cambagem da roda dianteira (Fig. 6).
: Ângulo de cambagem da roda dianteira (Fig. 6).
![]() ,
, ![]() ,
, ![]() : Deslocamentos angulares (Fig. 2).
: Deslocamentos angulares (Fig. 2).
Introdução
Estudos teóricos do comportamento de direção de automóveis após (Segel 1956) transformaram a compreensão do assunto e forneceram informações valiosas de projeto e técnicas de avaliação de projeto. Estudos paralelos relacionados a veículos de duas rodas (Whipple 1899) – (Collins 1964} foram comparativamente mal sucedidos, e o projeto de motocicletas atualmente depende da experiência em vez da compreensão para seu sucesso.
Uma teoria viável de estabilidade e controle de motocicletas deve ser consistente com a instabilidade praticamente óbvia da máquina em velocidades muito baixas, com a possibilidade de controle “sem intervenção” (ou seja, controle sem a aplicação direta do torque de direção) em velocidades moderadas e com a possível ocorrência de instabilidades oscilatórias em altas velocidades. Estas foram descritas por Pearsall (Pearsall 1922} como “oscilação do velocista” (Speedman’s Wobble). Ela também deve fornecer alguma explicação para a prática de design atual, ciente de que deve convergir para algum ótimo evolucionário e, idealmente, deve apoiar as máximas empíricas do design de motocicletas (por exemplo, o centro de massa deve ser o mais baixo possível e o mais à frente possível).
No caso do carro, (Segel 1964) observou que diferentes motoristas empregam diferentes proporções de controle fixo e livre, e que motoristas específicos podem alterar essas proporções para se adequarem ao carro que estão dirigindo. No caso da motocicleta, o comportamento de controle livre parece ser relativamente muito mais importante, uma vez que os ângulos de direção muito pequenos normalmente empregados (Wilson 1951) tornariam o controle fixo difícil, e uma vez que na condição de “mãos livres” as características de controle fixo da máquina não têm relevância para o movimento.
Consequentemente, o trabalho que é o assunto deste artigo foi direcionado para o desenvolvimento de um modelo matemático adequado de uma motocicleta em controle livre, e o uso de tal modelo para mostrar características típicas de estabilidade e como essas características dependem de vários valores de parâmetros. Além disso, à luz da conclusão de Segel\cite{segel1964} de que o gradiente de força de controle em estado estacionário é um parâmetro importante na determinação da qualidade de manuseio do carro, e sua declaração de que este é o caso também com aeronaves, foi estudado o comportamento em estado estacionário. O modelo é facilmente aplicado ao caso de controle fixo e os resultados apropriados são incluídos.
Uma dificuldade particular na análise diz respeito ao tratamento do comportamento do pneu. Whipple (Segel 1964, Pearsall 1922) e (Collins 1964) não permitiram aos pneus nenhuma liberdade de deslizamento lateral, enquanto Kondo, Nagaoka e Yoshimura (Kondo 1963) permitiram essa liberdade, mas ignoraram o atraso entre a direção de uma roda com pneu e o acúmulo da força lateral em direção a um valor de estado estacionário, o que é de grande importância no fenômeno de trepidação da roda (Pacejka 1966). Os resultados dependentes de cada uma das três suposições alternativas sobre o comportamento do pneu são incluídos e comparados.
DESCRIÇÃO FÍSICA DO MODELO
As seguintes suposições são feitas em relação à representação do veículo.
(1) O veículo consiste em duas estruturas rígidas unidas no eixo de direção com liberdade, restringida por um amortecedor de direção linear, da estrutura frontal para dirigir em relação à traseira.
(2) A estrutura frontal consiste na roda dianteira, garfos, guidão e acessórios.
(3) A estrutura traseira consiste na estrutura principal, o conjunto motor-caixa de câmbio, o tanque de gasolina, assento, garfos traseiros, roda traseira, etc., com o piloto rigidamente preso.
(4) Cada estrutura tem um plano longitudinal de simetria, e o eixo através do centro de massa da estrutura frontal paralelo ao eixo de direção é o principal.
(5) As rodas da estrada são discos rígidos, cada um fazendo contato pontual com a estrada, e rolam sem deslizamento longitudinal em uma superfície plana e nivelada da estrada.
(6) O eixo de rotação do volante do motor é transversal.
(7) A máquina se move a uma velocidade constante para frente com liberdade para derrapar, guinar e rolar; apenas pequenas perturbações da corrida em linha reta são consideradas.
(8) O ar através do qual a máquina se move é estacionário, de modo que os efeitos da força lateral aerodinâmica, momento de guinada e momento de rolamento serão pequenos em comparação com os efeitos dos pneus. Os efeitos do arrasto, sustentação e momento de arremesso são para modificar a carga vertical dos pneus e tornar necessária uma força longitudinal na roda motriz suficiente para manter a velocidade constante para frente assumida. Esses efeitos são contabilizados por variações nos coeficientes que relacionam as forças laterais do pneu aos ângulos de derrapagem e cambagem.
(9) O rastro pneumático dos pneus não é considerado, pois, para o pneu traseiro, seu efeito será muito pequeno e, para o pneu dianteiro, é pequeno em comparação com o rastro mecânico, e os efeitos da variação do próprio rastro mecânico estão incluídos nos resultados.
(10) A força de arrasto no pneu dianteiro é pequena em comparação com as forças laterais do pneu.
As suposições de que a motocicleta com rodas rígidas se move em uma superfície plana da estrada e que não tem liberdade para inclinar são, estritamente falando, incompatíveis. Conforme o guidão é virado, o ponto de contato do pneu dianteiro com a estrada em geral se move verticalmente e o problema é, de fato, tratado como se a superfície da estrada também se movesse verticalmente para manter o contato. Tendo em mente a pequenez desses movimentos verticais em funcionamento normal, e o fato de que as flexibilidades do pneu e da suspensão e as irregularidades da estrada foram ignoradas, isso é considerado uma extensão insignificante das suposições acima.
A motocicleta é representada no diagrama da Fig.1 com o ponto ![]() definido como a intersecção do plano transversal vertical contendo o centro de massa do chassi traseiro, o plano longitudinal de simetria e o plano do solo.
definido como a intersecção do plano transversal vertical contendo o centro de massa do chassi traseiro, o plano longitudinal de simetria e o plano do solo. ![]() é a origem de um conjunto de eixos ortogonais à direita
é a origem de um conjunto de eixos ortogonais à direita ![]() que se move com o veículo e que, com o veículo na condição de dado vertical, tem
que se move com o veículo e que, com o veículo na condição de dado vertical, tem ![]() horizontal e apontando para frente,
horizontal e apontando para frente, ![]() horizontal e para estibordo e
horizontal e para estibordo e ![]() verticalmente para baixo.
verticalmente para baixo.

O centro de massa do chassi dianteiro ![]() é a origem de outro conjunto de eixos ortogonais à direita
é a origem de outro conjunto de eixos ortogonais à direita ![]() , este se movendo com o chassi dianteiro. Com o veículo em sua condição de referência,
, este se movendo com o chassi dianteiro. Com o veículo em sua condição de referência, ![]() fica no plano longitudinal de simetria e é normal ao eixo de direção,
fica no plano longitudinal de simetria e é normal ao eixo de direção, ![]() é paralelo a
é paralelo a ![]() e
e ![]() é paralelo ao eixo de direção (apontando para baixo). O movimento da motocicleta é referido aos eixos inerciais
é paralelo ao eixo de direção (apontando para baixo). O movimento da motocicleta é referido aos eixos inerciais ![]() pelas coordenadas
pelas coordenadas ![]() ,
, ![]() de
de ![]() e os deslocamentos angulares
e os deslocamentos angulares ![]() ,
, ![]() e
e ![]() mostrados na Fig.2,
mostrados na Fig.2, ![]() sendo fixo na superfície da estrada.
sendo fixo na superfície da estrada.

EQUAÇÕES DE MOVIMENTO
As equações de movimento são derivadas pela aplicação da equação de Lagrange \cite{bishop1960}
(1) ![]()
A posição do veículo é definida em relação aos eixos ![]() pelas coordenadas
pelas coordenadas ![]() ,
, ![]() de
de ![]() , o ângulo de guinada e o ângulo de rolagem 4, que definem o chassi traseiro, o ângulo de direção
, o ângulo de guinada e o ângulo de rolagem 4, que definem o chassi traseiro, o ângulo de direção
![]() , que define o chassi dianteiro em relação ao traseiro, e os ângulos
, que define o chassi dianteiro em relação ao traseiro, e os ângulos
![]() e
e ![]() que definem as posições rotacionais das rodas da estrada e do volante do motor. Os últimos são mostrados nas Figuras 3 e 4. Expressões para as energias cinética e potencial em termos dessas sete coordenadas são primeiro obtidas e então utilizadas para fornecer equações para as liberdades lateral, de guinada, de rolagem e de direção da máquina.
que definem as posições rotacionais das rodas da estrada e do volante do motor. Os últimos são mostrados nas Figuras 3 e 4. Expressões para as energias cinética e potencial em termos dessas sete coordenadas são primeiro obtidas e então utilizadas para fornecer equações para as liberdades lateral, de guinada, de rolagem e de direção da máquina.

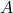 e roda traseira olhando
e roda traseira olhandoao longo de
 .
.

ao longo de
 .
.A exigência de uma equação que descreva o movimento longitudinal da motocicleta e de equações que descrevam as rotações das rodas desaparece por meio das suposições de velocidade constante para frente e de ausência de deslizamento longitudinal dos pneus; estas últimas também permitem a eliminação de ![]() e
e ![]() das outras equações.
das outras equações.
As forças generalizadas são derivadas em termos das forças do pneu. As forças do pneu são então obtidas em termos dos parâmetros de movimento do veículo, por meio de expressões para os ângulos de deslizamento lateral e cambagem do pneu. A consideração de pequenas perturbações da corrida em linha reta permite a eliminação de todos os termos de segunda ordem e de ordem superior; as equações finais do movimento são lineares.
As equações que descrevem a curva estável são obtidas pela eliminação dos termos variáveis no tempo, enquanto as equações de controle fixo são obtidas pela omissão do grau de liberdade da direção. Detalhes das derivações são fornecidos no Apêndice 1, enquanto no Apêndice 2 é mostrado como a análise pode ser restringida pela omissão do deslizamento lateral do pneu.
Solução das equações
As equações diferenciais lineares de movimento na forma homogênea, ou seja, com ![]() , foram reduzidas a um conjunto de equações de primeira ordem pela introdução de novas variáveis
, foram reduzidas a um conjunto de equações de primeira ordem pela introdução de novas variáveis ![]() ,
, ![]() ,
, ![]() e
e ![]() . Então, assumindo soluções da forma
. Então, assumindo soluções da forma ![]() ,
, ![]() , etc. (Karman 1940) e substituindo essas soluções de volta nas equações originais, resulta um conjunto de equações algébricas, que podem ser expressas na forma matricial
, etc. (Karman 1940) e substituindo essas soluções de volta nas equações originais, resulta um conjunto de equações algébricas, que podem ser expressas na forma matricial ![]() . Aqui,
. Aqui, ![]() e
e ![]() são matrizes de coeficientes quadrados, enquanto
são matrizes de coeficientes quadrados, enquanto ![]() é uma matriz coluna das amplitudes desconhecidas
é uma matriz coluna das amplitudes desconhecidas ![]() ,
, ![]() , etc.
, etc.
Pré-multiplicando por ![]() e reorganizando,
e reorganizando,
(2) ![]()
e para soluções não triviais para ![]() , os valores possíveis de
, os valores possíveis de ![]() devem ser autovalores de
devem ser autovalores de ![]() (Crandall 1956). As partes reais dos autovalores indicam o amortecimento e as partes imaginárias as frequências naturais associadas aos vários modos normais.
(Crandall 1956). As partes reais dos autovalores indicam o amortecimento e as partes imaginárias as frequências naturais associadas aos vários modos normais.
Um procedimento numérico foi, portanto, empregado para calcular os elementos das matrizes ![]() e
e ![]() acima a partir dos parâmetros de projeto para uma máquina específica e de sua velocidade de avanço, formando
acima a partir dos parâmetros de projeto para uma máquina específica e de sua velocidade de avanço, formando ![]() , e encontrando seus autovalores por meio de um procedimento empregando o algoritmo
, e encontrando seus autovalores por meio de um procedimento empregando o algoritmo ![]() (Wilkinson 1965). As equações de estado estacionário linear foram resolvidas escolhendo uma velocidade de avanço e ângulo de rolagem e resolvendo simultaneamente para
(Wilkinson 1965). As equações de estado estacionário linear foram resolvidas escolhendo uma velocidade de avanço e ângulo de rolagem e resolvendo simultaneamente para ![]() ,
, ![]() e
e ![]() , e então usando a equação para a liberdade de direção para fornecer
, e então usando a equação para a liberdade de direção para fornecer ![]() .
.
RESULTADOS
Os resultados se enquadram em uma das quatro categorias que abrangem os seguintes pontos.
(1) Frequências naturais e características de amortecimento de uma máquina específica em controle livre de acordo com o modelo que exclui o deslizamento lateral do pneu, o modelo que inclui o deslizamento lateral do pneu, mas assume resposta instantânea do pneu e o modelo que inclui a dinâmica da resposta do pneu.
(2) Os efeitos das mudanças no design da máquina no modelo que inclui a dinâmica da resposta do pneu.
(3) O comportamento de curva estável (em baixa aceleração lateral) como uma função da velocidade de avanço e do design da máquina.
(4) Frequências naturais e características de amortecimento da motocicleta em controle fixo.
Os resultados da categoria (1) são mostrados nas Figuras 5 – 7, nas quais os fatores de amortecimento são plotados em relação à velocidade de avanço, com as frequências circulares de quaisquer modos oscilatórios mostrados em relação às partes apropriadas das curvas. Os resultados da categoria (2) são mostrados nas Tabelas 1, 2 e 3, cada uma dessas tabelas se preocupando com um modo de significância física. A Tabela 1 se refere a um modo não oscilatório no qual, quando instável, o movimento da motocicleta é como o de um navio emborcando. Para facilitar a referência, isso será chamado de modo “emborcar”, e as Tabelas 2 e 3 se referem aos modos oscilatórios que serão chamados de modos “tecer” e “oscilar”, respectivamente. Outros modos são fortemente amortecidos e, portanto, fisicamente sem importância, e os resultados detalhados referentes a eles não estão incluídos. Os resultados da categoria (3) são mostrados na Tabela 4, enquanto aqueles na categoria (4) são fornecidos na Fig.8.

DISCUSSÃO DOS RESULTADOS
Os resultados da análise completa com a dinâmica da resposta do pneu incluída (Fig.5) mostram que a motocicleta tem três modos fisicamente significativos, que são aqui chamados de modos de capotamento, tecelagem e oscilação. O modo de capotamento não é oscilatório; em baixa velocidade, é bem amortecido, mas tem amortecimento decrescente rapidamente à medida que a velocidade aumenta acima de 15 ft/s aproximadamente. Ele se torna muito levemente instável acima de cerca de 35 ft/s com taxa de divergência máxima próxima a 60 ft/s, diminuindo depois à medida que a velocidade aumenta. O modo de tecelagem tem uma frequência natural aumentando de cerca de 0,2 Hz a 5 ft/s de velocidade para frente para cerca de 3,4 Hz a 160 ft/s de velocidade para frente, é instável até cerca de 20 ft/s, bem amortecido na faixa de velocidade média e é moderadamente amortecido em alta velocidade. O modo oscilante tem uma frequência natural que é quase independente da velocidade de avanço e é de cerca de 9 Hz. É bem amortecido em velocidades baixas e médias, mas apenas moderadamente em altas velocidades. Este grau de amortecimento é fortemente dependente do valor tomado para o comprimento de relaxamento, ![]() (Tabela 3), e o do modo “onda” é um pouco assim (Tabela 2), e, como seria de se esperar, como
(Tabela 3), e o do modo “onda” é um pouco assim (Tabela 2), e, como seria de se esperar, como ![]() os resultados mostrados na Fig.5 se tornam mais próximos daqueles da Fig.6.
os resultados mostrados na Fig.5 se tornam mais próximos daqueles da Fig.6.

A Fig.6 mostra um modo de capotamento virtualmente idêntico ao da Fig.5, mas também mostra um amortecimento significativamente menor do modo de onda em alta velocidade e um amortecimento marcadamente diferente do modo de oscilação em toda a faixa de velocidade. As frequências naturais dos modelos com resposta instantânea do pneu e resposta dinâmica adequada do pneu são semelhantes.
A Fig.7 mostra que o modelo sem derrapagem do pneu fornece representações do modo de capotamento e, somente em baixas velocidades, do modo de onda, semelhantes aos do modelo completo. Com o modelo sem derrapagem, no entanto, o modo de oscilação está completamente ausente e nenhuma possibilidade de explicação do fenômeno de “oscilação do speedman” é oferecida.

O autor não tem conhecimento de nenhuma informação específica sobre comprimentos de relaxamento para pneus de motocicleta, e o valor de 0,8 ft que foi tomado para a máquina padrão é baseado principalmente em medições de Labarre e Mills \cite{labarre1968} em um pneu de 2![]() in de seção e 12
in de seção e 12![]() in de diâmetro. Se esse valor for da ordem de grandeza correta, o que é muito provável, é aparente que uma representação adequada das características dinâmicas da motocicleta depende da inclusão do deslizamento lateral do pneu e da propriedade de relaxamento do pneu.
in de diâmetro. Se esse valor for da ordem de grandeza correta, o que é muito provável, é aparente que uma representação adequada das características dinâmicas da motocicleta depende da inclusão do deslizamento lateral do pneu e da propriedade de relaxamento do pneu.

Os efeitos de parâmetros registrados nas Tabelas 1, 2 e 3 mostram que o modo de capotamento é comparativamente pouco alterado, mas os modos de tecelagem e oscilação podem ser influenciados consideravelmente por mudanças de parâmetros. O último é mais sensível ao coeficiente de amortecimento de direção, ![]() , aumentando o que estabiliza a oscilação às custas do modo de tecelagem, embora as mudanças no último com a variação de
, aumentando o que estabiliza a oscilação às custas do modo de tecelagem, embora as mudanças no último com a variação de ![]() não sejam grandes. Ao aumentar o amortecimento de direção, de fato, o amortecimento adequado do modo de oscilação em qualquer velocidade (até o máximo de 160 ft/s empregado neste estudo) pode ser obtido, de modo que o problema potencial em alta velocidade é o amortecimento inadequado do modo de tecelagem. O comprimento de relaxamento também é um parâmetro importante, como já indicado, e aumentá-lo desestabiliza os modos de tecelagem e oscilação apreciavelmente.
não sejam grandes. Ao aumentar o amortecimento de direção, de fato, o amortecimento adequado do modo de oscilação em qualquer velocidade (até o máximo de 160 ft/s empregado neste estudo) pode ser obtido, de modo que o problema potencial em alta velocidade é o amortecimento inadequado do modo de tecelagem. O comprimento de relaxamento também é um parâmetro importante, como já indicado, e aumentá-lo desestabiliza os modos de tecelagem e oscilação apreciavelmente.
APÊNDICE 1
DERIVAÇÃO DAS EQUAÇÕES DE MOVIMENTO
Energia cinética
(3) ![]()
Com
(4) ![]()
(5) 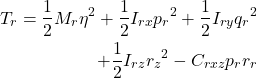
e ![]() termos extras além daqueles incluídos em
termos extras além daqueles incluídos em ![]() e
e ![]() para levar em conta as rotações das rodas e do volante do motor.
para levar em conta as rotações das rodas e do volante do motor.
![]() tem componentes de velocidade
tem componentes de velocidade
![Rendered by QuickLaTeX.com \[ \left\{ \begin{aligned} & \dot{x}_1 - h sin \phi \dot{\psi} \\ & \dot{y}_1 + h cos \phi\dot{\phi} \\ & h sin \phi\dot{\phi} \end{aligned} \right\} \quad \begin{aligned} &\text{ao longo de $OX_1$} \\ &\text{ao longo de $OY_1$} \\ &\text{ao longo de $OZ_1$} \end{aligned} \]](https://renanxyz.com.br/wp-content/ql-cache/quicklatex.com-72d059814ee647d04296b09bbc37bafe_l3.png)
portanto
(6) ![]()
também
![]() ,
, ![]() ,
, ![]()
portanto
(7) 
(8) ![Rendered by QuickLaTeX.com \begin{eqnarray*} \begin{aligned} T_f = \frac{1}{2}M_r[\{\dot{x}_1 - ecos \epsilon sin \delta \dot{\delta} - (a sin\epsilon \phi \\ + e sin \delta cos \phi + e sin \epsilon cos \delta sin \phi \\ + f cos \epsilon sin\phi)\dot{\psi}}^2 + {\dot{y}_1 + a sin \epsilon cos \phi \dot{\phi}\\ + e sin \epsilon cos \delta cos \phi \dot{\phi} - e sin \epsilon sin \delta sin \phi \delta{\delta}\\ + f cos \epsilon cos \phi \dot{phi} + (a cos \epsilon + e cos \epsilon cos \delta\\ - f sin \epsilon) \dot{\psi}^2} + {a sin \epsilon sin \phi \dot{\phi} + e sin \delta cos \phi \dot{\phi}\\ + e cos \delta sin \phi \dot{\delta} + e sin \epsilon cos \delta sin \phi \dot{\phi}\\ + e sin\epsilon sin\delta cos\phi \dot{\delta} + f cos\epsilon sin\phi \dot{\phi}\}^2]\\ + \frac{1}{2}I_{fx}\{cos\epsilon cos \delta \dot{\phi} + (sin\delta sin\phi\\ - sin\epsilon cos\delta cos\phi)\dot{\psi}\}^2 + \frac{1}{2}I_{fy}\{-cos\epsilon sin \delta \dot{\phi}\\ + sin\epsilon sin\delta cos\phi + cos\delta sin\phi)\dot{\psi}\}^2\\ + \frac{1}{2} I_{fz}\{\dot{\delta} + sin \epsilon \dot{\phi} + cos\epsilon cos\phi \dot{\psi}\}^2 \end{aligned} \end{eqnarray*}](https://renanxyz.com.br/wp-content/ql-cache/quicklatex.com-86320474f012ccfed6f6ce3dc7491c9d_l3.png)
As energias cinéticas de translação das rodas são contabilizadas em ![]() e
e ![]() , mas as energias cinéticas de rotação não.
, mas as energias cinéticas de rotação não.
Para a roda traseira, os componentes da velocidade angular nos eixos ![]() são
são
![Rendered by QuickLaTeX.com \[ \left\{ \begin{aligned} & P_r \\ & q_r + \dot{\theta_r} \\ & r_r \end{aligned} \right\} = \left\{ \begin{aligned} & \phi \\ & \sin\phi \dot{\psi} + \dot{\theta_r} \\ & cos\phi \dot{\psi} \end{aligned} \right\} \]](https://renanxyz.com.br/wp-content/ql-cache/quicklatex.com-6127fe137b17fbdd41dec59877473d76_l3.png)
energia cinética rotacional ![]()
Esses termos já foram contabilizados pela inclusão da roda traseira no quadro traseiro, exceto ![]() e, portanto, esse termo contribui para
e, portanto, esse termo contribui para ![]() .
.
Da mesma forma, o volante do motor e a roda dianteira contribuem com ![]() para que
para que
(9) ![Rendered by QuickLaTeX.com \begin{eqnarray*} \begin{aligned} T_{\omega} = \textbf{i}_{ry}(sin \phi \dot{\psi} \dot{\theta_r} + \frac{1}{2}\dot{\theta_r}^2) + i(\lambda sin\phi \dot{\psi} \dot{\theta_r} + \frac{1}{2}\lambda^2 \dot{\theta_r}^2) \\ \textbf{i}_{fy}[\{-cos \epsilon sin\delta \dot{\phi} + (sin \epsilon sin\delta cos\phi\\ + cos \delta sin\phi)\dot{\psi}\}\dot{\theta_f} + \frac{1}{2}\dot{\theta_f}^2] \end{aligned} \end{eqnarray*}](https://renanxyz.com.br/wp-content/ql-cache/quicklatex.com-4fb12010c730db021231f0c30ff0e77f_l3.png)
\noindent dando ![]() pela adição das equações (7), (8) e (9).
pela adição das equações (7), (8) e (9).
Energia potencial
![]() e inclui apenas a energia potencial gravitacional
e inclui apenas a energia potencial gravitacional
dos quadros dianteiro e traseiro, tomada como zero quando ambos
os centros de massa estão no nível do solo. Portanto
(10) ![]()
\textbf{Equação lateral do movimento} e ![]()
As equações para a translação do veículo ao longo de ![]()
e ![]() reduzem-se
reduzem-se
(11) ![]()
respectivamente, desde
(12) ![]()
A inércia e as forças externas são resolvidas ao longo de ![]() para obter a equação lateral do movimento, portanto
para obter a equação lateral do movimento, portanto
(13) ![]()
(14) ![]()
Por meio do uso dessas expressões (13) e (14), evita-se a necessidade de substituir ![]() e
e ![]() por
por ![]() e
e ![]() na expressão de energia cinética.\\
na expressão de energia cinética.\\
\textbf{Eliminação de} ![]() e
e ![]()
Para nenhum deslizamento longitudinal do pneu
(15) ![]()
O ponto mais baixo da circunferência da roda dianteira, ou seja, o ponto de contato pneu-estrada, tem
(16) ![]()
ignorando o termo de segunda ordem ![]() .
.
Igualando a componente de velocidade ao longo de ![]() de um ponto geral na circunferência da roda dianteira, com a condição acima
de um ponto geral na circunferência da roda dianteira, com a condição acima ![]() , a zero, obtém-se
, a zero, obtém-se
(17) ![]()

Forças generalizadas
Em referência à Fig.9
(18) ![]()
e usando a equação (16)
(19) ![]()
(20) ![]()
(21) ![]()
substituindo ![]() por
por ![]() e colocando cos
e colocando cos ![]() . A carga da roda dianteira
. A carga da roda dianteira ![]() é tomada como constante.
é tomada como constante.
Forças laterais do pneu
As forças laterais do pneu são funções dos respectivos ângulos de deslizamento lateral e cambagem dos pneus. A roda dianteira em alguma posição geralmente deslocada é mostrada na Fig.10 com ![]() o vetor unitário ao longo do eixo da roda.
o vetor unitário ao longo do eixo da roda.

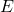 ,
,  e
e 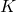 é paralelo ao plano de solo
é paralelo ao plano de solo  ,
,  , com
, com 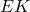 paralelo a
paralelo a 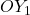
![Rendered by QuickLaTeX.com \[ EI \hspace{2mm}\text{tem componentes} \left\{ \begin{aligned} & - \delta cos \epsilon \\ & cos \phi - sin \epsilon sin \phi \delta \\ & sin \phi + sin \epsilon cos \phi \delta \end{aligned} \right\} \quad \begin{aligned} &\text{ao longo de $OX_1$} \\ &\text{ao longo de $OY_1$} \\ &\text{ao longo de $OZ_1$} \end{aligned} \]](https://renanxyz.com.br/wp-content/ql-cache/quicklatex.com-1d22ea138db9a7d94f5342cd719f27b8_l3.png)
Portanto
(22) ![]()
e
(23) ![]()
A velocidade de avanço do ponto de contato do pneu dianteiro é
(24) ![]()
usando a equação (16) e ![]() . A velocidade lateral é
. A velocidade lateral é
(25) ![]()
novamente usando a equação (16). Portanto
(26) ![Rendered by QuickLaTeX.com \begin{eqnarray*} \begin{aligned} \alpha_f \simeq tan^{-1} \left[\frac{1}{\dot{x}_1}\{\dot{y}_1 + l\dot{\psi} + t(\delta sin\phi\dot{\psi} - \dot{\delta}cos\phi)\}\right] - \gamma \\ \text{e} \hspace{4mm} \alpha_r \simeq tan^{-1} \left[\frac{1}{\dot{x}_1}(\dot{y}_1 + b\dot{\psi})\right] \end{aligned} \end{eqnarray*}](https://renanxyz.com.br/wp-content/ql-cache/quicklatex.com-93db84494eb172abf7bdbe032f7d65a1_l3.png)
com o ângulo de cambagem da roda traseira simplesmente ![]() .
.
Quando os ângulos de deslizamento lateral e de cambagem são pequenos, as forças laterais do pneu em estado estacionário são descritas com precisão por funções lineares de deslizamento lateral e ângulos de cambagem da forma
(27) ![]()
(28) ![]()
e as forças laterais do pneu ![]() e
e ![]() estão relacionadas aos seus valores de estado estacionário pelas equações (17)
estão relacionadas aos seus valores de estado estacionário pelas equações (17)
(29) ![]()
quando a propriedade de relaxamento do pneu é contabilizada. Esta propriedade é omitida da análise colocando ![]() e
e ![]() em vez das equações (29).
em vez das equações (29).
Equações lineares de movimento
Diferenciações apropriadas da expressão para ![]() (por
(por
adição das equações (7), (8) e (9)) e ![]() (equação (10)), dão
(equação (10)), dão ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() e, da equação (14),
e, da equação (14), ![]() . As forças generalizadas são dadas nas equações (18), (19), (20) e (21), as forças laterais do pneu nas equações (27)-(29), e os ângulos de deslizamento lateral e cambagem nas equações (22)-(26). Assim, todos os termos necessários para a equação lateral (13) e para as outras três equações na forma padrão (equação (??)) estão disponíveis.
. As forças generalizadas são dadas nas equações (18), (19), (20) e (21), as forças laterais do pneu nas equações (27)-(29), e os ângulos de deslizamento lateral e cambagem nas equações (22)-(26). Assim, todos os termos necessários para a equação lateral (13) e para as outras três equações na forma padrão (equação (??)) estão disponíveis.
Com os termos de segunda e de ordem superior omitidos, as equações são
(30) 
(31) 
(32) 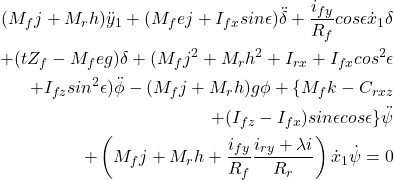
(33) 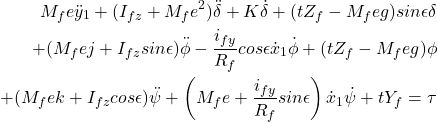
(34) 
APÊNDICE 2
Equações de movimento com deslizamento lateral do pneu eliminado
A condição de que os pneus não derrapem implica que ![]() . Assim, a partir das equações (23) e (26)
. Assim, a partir das equações (23) e (26)
(35) ![]()
e ![]() , dando
, dando
(36) ![]()
e portanto
(37) ![]()
para ![]() constante.
constante.
Substituindo essas expressões nas equações lineares de movimento e eliminando ![]() e
e ![]() obtemos
obtemos
(38) ![Rendered by QuickLaTeX.com \begin{eqnarray*}\nonumber \begin{aligned} [(M_{f}j + M_{r}h)b t + M_{f} e j l_1 + I_{fz} \sin \epsilon l_1 \\ + \left\{M_{f}j k - C_{rxz} + (I_{fz} - I_{fx}) \sin \epsilon \cos \epsilon \right\} t ] \ddot{\delta} \\ + \bigg[(M_{f}j + M_{r}h) b \cos \epsilon \dot{x}_1 + \frac{I_{fy}}{R_f} \dot{x}_1 \cos \epsilon l_1 \\ + \left\{M_{f}j k - C_{rxz} + (I_{fz} - I_{fx}) \sin \epsilon \cos \epsilon \right\} \dot{x}_1 \cos \epsilon \\ + \left(M_{f}j + M_{r}h + \frac{i_{fy}}{R_f} + \frac{i_{fy} + \lambda i}{R_r}\right) \dot{x}_1 t \bigg] \dot{\delta} + \bigg[-M_{f} e l_1 g \\ + \left(M_{f}j + M_{r}h + \frac{i_{fy}}{R_f} + \frac{i_{fy + \lambda i}}{R_r}\right) x_1^2 \cos \epsilon + Z_f t l_1 \bigg] \delta \\ + \left(M_{f} j^2 + M_{r} h^2 + I_{rx} + I_{fx} \cos^2 \epsilon + I_{fz} \sin^2 \epsilon \right) l_1 \ddot{\phi} \\ - (M_{f} j + M_{r} h) g l_1 \phi = 0 \end{aligned} \end{eqnarray*}](https://renanxyz.com.br/wp-content/ql-cache/quicklatex.com-333fd35a018d9e6326daa4d2149340ab_l3.png)
e
(39) ![Rendered by QuickLaTeX.com \begin{eqnarray*}\nonumber \begin{aligned} [I_{fz} {l_1}^2 + M_f e^2 {l_1}^2 + t^2 \{(M_f + M_r)b^2 + 2 M_f bk + M_fk^2 + I_{rz}\\ + I_{fx} sin^2 \epsilon + I_{fz} cos^2 \epsilon\}]\ddot{\delta} + \bigg[ M_f ebl_1 \dot{x}_1 cos \epsilon \\ + (M_f ek + I_{fz} cos \epsilon)l_1 \dot{x}_1 cos\epsilon + \left(M_fe + \frac{i_{fy}}{R_f} sin \epsilon \right)\dot{x}_1 l_1 t \\ + K {l_1}^2 + t\{(M_f + M_r)b^2 \dot{x}_1 cos\epsilon + 2 M_f bk \dot{x}_1 cos\epsilon \\ + (M_f + M_r)bt \dot{x}_1 - \frac{i_{fy}}{R_f}l_1 \dot{x}_1 sin \epsilon + (M_f k^2 + I_{rz} + I_{fx} sin^2 \epsilon \\ + I_{fz} cos^2 \epsilon)\dot{x}_1 cos\epsilon + M_f kt \dot{x}_1 \}\bigg]\dot{\delta} + \bigg[Z_f t {l_1}^2 sin\epsilon - M_f e{l_1}^2 g sin\epsilon \\ +\left(M_f e + \frac{i_{fy}}{R_f} sin \epsilon \right)\dot{x_1}^2 l_1 cos\epsilon + t \{(M_f + M_r)\dot{x_1}^2 b cos \epsilon \\ + M_f k \dot{x_1}^2 cos \epsilon \}\bigg]\delta + [M_f ej {l_1}^2 - I_{fz} {l_1}^2 sin\epsilon + b l_1 t(M_f j + M_r h) \\ + tl_1 \{M_f jk - C_{rxz} + (I_{fz} - I_{fx})sin\epsilon cos\epsilon \}] \ddot{\phi} + \bigg[- \frac{i_{fy}}{R_f} l_1 cos \epsilon \\ - t \left(\frac{i_{fy}}{R_f} + \frac{i_{fy} + \lambda i}{R_r}\right)\bigg]l_1\dot{x}_1 \dot{\phi} + (Z_f t - M_f eg){l_1}^2 \phi = 0 \end{aligned} \end{eqnarray*}](https://renanxyz.com.br/wp-content/ql-cache/quicklatex.com-59d6c5f44e679f3a26d3dbed9085b3bf_l3.png)
APÊNDICE 3
Valores de parâmetros a máquina padrão e o condutor
![]() 2.1 slug.
2.1 slug.
{![]() 14.9 slug.}
14.9 slug.}
![]() -226 lb.
-226 lb.
![]() 23 slug ft
23 slug ft![]() .
.
![]() 15.54 slug ft
15.54 slug ft![]() .
.
![]() 1.28 slug ft
1.28 slug ft![]() .
.
![]() 0.91 slug ft
0.91 slug ft![]() .
.
![]() 0.326 slug ft
0.326 slug ft![]() .
.
![]() 0.53 slug ft
0.53 slug ft![]() .
.
![]() 0.775 slug ft
0.775 slug ft![]() .
.
![]() 3.112 ft.
3.112 ft.
![]() 1.574 ft.
1.574 ft.
![]() 0.08 ft.
0.08 ft.
![]() 0.093 ft.
0.093 ft.
![]() 2.02 ft.
2.02 ft.
![]() ,
, ![]() 1 ft.
1 ft.
![]() 0.38 ft.
0.38 ft.
![]() 0.4715 rad = 27°.
0.4715 rad = 27°.
![]() 2512 lb/rad.
2512 lb/rad.
![]() 211 lb/rad.
211 lb/rad.
![]() 3559 lb/rad.
3559 lb/rad.
![]() 298 Ib/rad.
298 Ib/rad.
![]() 5 lb ft/(rad/s).
5 lb ft/(rad/s).
![]() 0.8 ft.
0.8 ft.
APÊNDICE 4
Números chaves para o modelo
(1) Máquina padrão (valores de parâmetros no Apêndice 3).
(2) Amortecimento de direção reduzido, ![]() = 2 lb ft/(rad/s).
= 2 lb ft/(rad/s).
(3) Amortecimento de direção aumentado, ![]() = 10 lb ft/(rad/s).
= 10 lb ft/(rad/s).
(4) Comprimento de relaxamento curto, ![]() = 0,4 ft.
= 0,4 ft.
(5) Comprimento de relaxamento longo, ![]() = 1,4 ft.
= 1,4 ft.
(6) Centro de massa do chassi traseiro baixo, ![]() = 1,01 ft.
= 1,01 ft.
(7) Centro de massa do chassi traseiro movido 1 ft para frente com ![]() = 8 lb ft/(rad/s).
= 8 lb ft/(rad/s).
(8) Centro de massa do chassi dianteiro movido para trás, ![]() = -0,12 ft, com
= -0,12 ft, com ![]() = 8 lb ft/(rad/s).
= 8 lb ft/(rad/s).
(9) Centro de massa do chassi dianteiro movido para baixo, ![]() = -0,41 pés.
= -0,41 pés.
(10) Cabeçote de direção íngreme, ![]() = 19°, com trilha curta,
= 19°, com trilha curta, ![]() = 0,18 pés.
= 0,18 pés.
(11) Cabeçote de direção íngreme, ![]() = 19°.
= 19°.
(12) Cabeçote de direção íngreme, ![]() = 19°, com trilha longa, t = 0,58 pés.
= 19°, com trilha longa, t = 0,58 pés.
(13) Trilha curta, ![]() = 0,18 pés.
= 0,18 pés.
(14) Trilha longa, ![]() = 0,58 pés.
= 0,58 pés.
(15) Cabeçote de direção raso, ![]() = 35°, com trilha curta,
= 35°, com trilha curta, ![]() = 0,18 pés.
= 0,18 pés.
(16) Cabeçote de direção raso, ![]() = 35°.
= 35°.
(17) Cabeça de direção rasa, ![]() = 35°, com trilha longa,
= 35°, com trilha longa, ![]() = 0,58 ft.
= 0,58 ft.
(18) Inércia da roda dianteira reduzida, ![]() = 0,265 slug ft
= 0,265 slug ft![]() , com
, com ![]() = 3 lb ft/(rad/s).
= 3 lb ft/(rad/s).
(19) Inércia da roda dianteira aumentada, ![]() = 1,06 slug ft
= 1,06 slug ft![]() , com
, com ![]() = 7,5 lb ft/(rad/s).
= 7,5 lb ft/(rad/s).
(20) Inércia da roda traseira aumentada, ![]() = 1,55 slug ft
= 1,55 slug ft![]() , com K = 6 lb ft/(rad/s).
, com K = 6 lb ft/(rad/s).
(21) Centro do cubo esterçado com ângulo de rodízio de 15°.
(22) Centro do cubo esterçado com ângulo de rodízio de 25°.
(23) Centro do cubo esterçado com ângulo de castor de 35°.
(24) Com passageiro na garupa e K = 4 lb ft/(rad/s).
(25) Roda traseira movida 0,5 ft para trás para aumentar a distância entre eixos, com K = 6 lb ft/(rad/s).
(26) ![]() reduzido em 20 por cento para 2010 lb/rad.
reduzido em 20 por cento para 2010 lb/rad.
(27) ![]() reduzido em 20 por cento para 169 lb/rad.
reduzido em 20 por cento para 169 lb/rad.
(28) ![]() reduzido em 20 por cento para 2847 lb/rad.
reduzido em 20 por cento para 2847 lb/rad.
(29) ![]() reduzido em 20 por cento para 238 lb/rad.
reduzido em 20 por cento para 238 lb/rad.
(30) ![]() reduzido em 20 por cento para 18,4 slug ft
reduzido em 20 por cento para 18,4 slug ft![]() .
.
REFERÊNCIAS
[1] SEGEL, L. “Theoretical prediction and experimental substantiation of the response of the automobile to steering control”. Em: Proc. Auto. Div. Instn mech. Engrs No 7 (1956-57), p. 310.
[2] WHIPPLE, F. J. W. “The stability of the motion of the bicycle”. Em: Q. 3. Math. 30 (1989), p. 312.
[3] COLLINS, R. N. “A mathematical analysis of the stability of two-wheeled vehicles”. Em: (University Microfilms Inc., Ann Arbor, Michigan) (1964).
[4] PEARSALL, R. H. “The stability of a bicycle”. Em: Proc. Instn Auto. Engrs 17 (1922), p. 395.
[5] SEGEL, L. “An investigation of automobile handling as implemented by a variable-steering automobileEm: Hum. Factors 6 (1964), p. 333.
[6] WILSON-JONES, R. A. “Steering and stability of single track vehicles”. Em: Proc. Auto. Div. Instn mech.
Engrs (1951-52), p. 191.
[7] KONDO M., N. A. e YOSHIMURA, F. “Theoretical study on the running stability of the two-wheelers”. Em: Trans. Soc. auto. Engrs Japan 17 (No.1) (1963), p. 8.
[8] PACEJKA, H. B. “Analysis of the shimmy phenomenon”. Em: Proc. Instn mech. Engrs Pt 2A.180 (1965-66), p. 251.
[9] BISHOP, R. E. D. e JOHNSON, D. C. “The mechanics of vibration”. Em: (Cambridge University Press)
(1960).
[10] KARMAN, T. V. e BIOT, M. A. “Mathematical methods in engineering: an introduction to the mathematical treatment of engineering problems”. Em: (McGraw-Hill, Inc., New York and London) (1940).
[11] CRANDALL, S. H. “Engineering analysis: a survey of numerical procedures”. Em: (McGraw-Hill, Inc., New York and London) (1956).
[12] WILKINSON, J. H. “The algebraic eigenvalue problem”. Em: (Clarendon Press, Oxford) (1965).
[13] LABARRE, R. P. e MILLS, B. “An investigation into the dynamic stability of steering systems”. Em: Proc. Instn mech. Engrs Pt 2A.183 (1968-69), p. 113.
Tabelas



