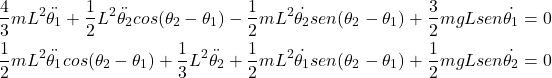Equações de Movimento e de Lagrange
Para o pêndulo duplo mostrado na figura, as barras de ligações 1 e 2 (barras ![]() e
e ![]() ) são homogêneas e têm os comprimentos
) são homogêneas e têm os comprimentos ![]() ,
, ![]() e as massas
e as massas ![]() , o
, o ![]() . Em
. Em ![]() e
e ![]() há pinos nas juntas. Os centros de massa das ligações 1 e 2 são
há pinos nas juntas. Os centros de massa das ligações 1 e 2 são ![]() e
e ![]() . Localize e resolva as Equações de Lagrange e de movimento se o duplo pêndulo é liberado a partir do repouso quando os ângulos dos elos 1 e 2 em relação a vertical são
. Localize e resolva as Equações de Lagrange e de movimento se o duplo pêndulo é liberado a partir do repouso quando os ângulos dos elos 1 e 2 em relação a vertical são ![]() e
e ![]() .
.

Solução:
Para caracterizar a configuração do sistema, são empregados duas coordenadas generalizadas ![]() e
e ![]() . A coordenada
. A coordenada ![]() é a medida do ângulo em radianos do entre o eixo vertical e o elo 1 e
é a medida do ângulo em radianos do entre o eixo vertical e o elo 1 e ![]() é a medida do ângulo de rotação em radianos entre o elo 2 e a direção vertical. O vetor de posição de vetor de velocidade do centro de massa de
é a medida do ângulo de rotação em radianos entre o elo 2 e a direção vertical. O vetor de posição de vetor de velocidade do centro de massa de ![]() do elo 1 pode ser escrito como
do elo 1 pode ser escrito como
(1) ![]()
(2) ![]()
O vetor de posição de vetor de velocidade do centro de massa de ![]() do elo 2 pode ser escrito como
do elo 2 pode ser escrito como
(3) ![]()
(4) ![]()
As energias cinéticas da ligações 1 e 2 são
(5) ![]()
(6) ![]()
(7) ![]()
onde ![]() é o momento de inércia em torno do centro de rotação de O, e
é o momento de inércia em torno do centro de rotação de O, e ![]() é o momento de inércia em torno do centro de massa
é o momento de inércia em torno do centro de massa ![]()
A energia cinética total do sistema é
(8) ![]()
O lado esquerdo da equação de Lagrange é
(9) ![]()
(10) ![]()
(11) ![]()
(12) ![]()
(13) ![]()
(14) ![]()
As forças gravitacionais sobre as ligações 1 e 2 no centros de massa ![]() e
e ![]() são
são
(15) ![]()
Existem duas forças generalizadas associadas a ![]() e
e ![]() são
são
(16) ![Rendered by QuickLaTeX.com \begin{eqnarray*} F_1 &=& {\bf G}_1 \cdot \frac{\partial{\bf r}_{C_1}}{\partial \theta_1} + {\bf G}_2 \cdot \frac{\partial{\bf r}_{C_2}}{\partial \theta_1}\\ &=& mg {\bf j} \cdot \left[\frac{1}{2}L cos(\theta_1) {\bf i} - \frac{1}{2}L sen (\theta_1) {\bf i} \right]+ \;\;\;\;\;\;\;\;\ \\ &+& mg {\bf j} \cdot [L cos(\theta_1) {\bf i} - L sen (\theta_1) {\bf i}]\\ &=& -\frac{3}{2}mg L sen(\theta_1) \end{eqnarray*}](https://renanxyz.com.br/wp-content/ql-cache/quicklatex.com-1790a7de4c4db5ab0b01e04fd71a9aa8_l3.png)
(17) ![Rendered by QuickLaTeX.com \begin{eqnarray*} F_2 &=& {\bf G}_1 \cdot \frac{\partial{\bf r}_{C_1}}{\partial \theta_2} + {\bf G}_2 \cdot \frac{\partial{\bf r}_{C_2}}{\partial \theta_2}\\ &=& mg {\bf j}\cdot 0 + mg {\bf j} \cdot \left[\frac{1}{2}L cos(\theta_2) {\bf i} - \frac{1}{2}L sen (\theta_2) {\bf i} \right]\\ &=& -\frac{1}{2}mg L sen(\theta_2) \end{eqnarray*}](https://renanxyz.com.br/wp-content/ql-cache/quicklatex.com-d3b5599b10e60267c4315424c0f0b032_l3.png)
As equações de Lagrange são escritas como
(18) ![]()
(19) ![]()
e as equações de movimento pode ser escrita como
(20)