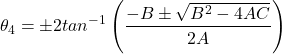Formulação
O ângulo 
é igual a 180º, o ângulo entre 
e 
é de 90º. 
é o ângulo entre os vetores 
e 
e representa um dado de entrada. A soma dos ângulos no ponto B é: 
+ (180º – 
) + 90º = 360º, então = 90º + .
O polígono formado pelos vetores na Figura 1 pode ser descrito por:
(1) 
Decompondo Eq. (1), torna-se:
(2) 
(3) 
Substituindo e , temos:
(4) 
(5) 
O valor de 
vem da Eq. (5) em função dos dados de entrada , 
e 
:
(6) 
Substituindo a Eq. (6) na Eq. (4):
(7) 
Simplificando, temos:
(8) 
O ângulo é determinado considerando os seguintes relações trigonométricas na Eq. (8):
(9) 
(10) 
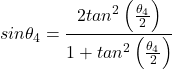
(11) 
Simplificando, teremos:
(12) 
Os coeficientes do polinômio do segundo grau da Eq. (13) são:
Então é dado por:
(13) 